Updated on October 10, 2025.
No responsibility is taken for the correctness or completeness of the information presented in this article.
Starglider 2 (SG2) is a computer game made by Argonaut Software and released in 1988 by the publisher Rainbird. In this game, you fly a small starship, the Icarus, in a planetary system consisting of 15 planets and moons. The goal is to destroy a space station built by your enemy, the Egrons, before they can use it to attack your home planet. To achieve this, you need to build a special bomb — a task for which various objects are needed that you have to find on the different planets and moons, in underground tunnel systems, and also sometimes in the inter-planetary space. Of course, all those places are populated with enemies that try to kill you.
SG2 is a fast paced game with smooth 3D graphics using flat shaded polygons. It was originally published for the Amiga and Atari ST platforms. Typical for the time, the game was completely written in assembly. Since both platforms use the Motorola 68000 CPU, they share the same code for everything that is not platform-specific. In fact, the same game disk was sold for both platforms and contained a single binary that checks during execution time on which platform it runs. The author of this article has never played the Atari ST version, but according to a magazine article cited on Wikipedia, it was running less smoothly than the Amiga version.
The planetary system in SG2 consists of the central star, Solice, and five planets, named Dante (the hottest planet closest to Solice), Vista, Apogee (your home planet), Millway, and Aldos. Apogee has two moons, Enos and Castron. Millway has seven moons called Broadway, Apex, Esprit, Questa, Westmere, Synapse, and Wackfunk. Aldos has only one moon Q-Beta.
 |
|---|
| The Icarus spaceship on the surface of Apogee. |
To win the game, you have to collect various objects. Some of them are only found on certain planets or moons, either on their surface or in underground tunnel systems. And some objects can only be found in the inter-planetary space that is populated with asteroids, pirates, and other interesting things.
In the following, we will call the different places you can visit with your spaceship, i.e. the inter-planetary space, the planets, the moons, and the tunnel systems, worlds. The game stores the ID of the world you are currently located in a 16-bit variable, where ID 0 stands for the inter-planetary space, ID 1 for Dante, ID 2 for Vista, and so on. Tunnel systems have IDs identical to the ID of the planet they are located on plus 128 (i.e. bit 7 is set), i.e. there can be only one tunnel system per planet or moon.
Although storing what is essentially an 8-bit value as a 16-bit variable might look wasteful to old school programmers, remember that the Motorola 68000 CPU has a 16-bit databus and therefore does 16-bit memory accesses with the same speed as 8-bit accesses.
Worlds are isolated from each other in the sense that each world has its own 3D coordinate system and enemies and other objects do not follow you when you leave one world and enter another, e.g. when you fly from space into a planet’s atmosphere. The coordinates of all objects in the game are represented by three 32-bit integers for x/y/z. Whenever an object moves, its x and z coordinates (i.e. the coordinates spanning the horizional plane) wrap around when they are outside the range , where is a world-specific maximum value. This is efficiently implemented by a binary AND operation as the maximum values are always powers of two. The below table shows the maximum value for the different worlds:
| World | |
|---|---|
| Space | |
| Dante, Vista, Apogee, Aldos | |
| Millway | |
| Moons of Apogee and Millway | |
| Q-Beta |
Wrapping around the coordinates in this way has a very important practical effect on the gameplay: it turns the planet and moon surfaces into tori, and if you fly straight for long enough, you will arrive back at your starting point. In combination with a short viewing distance, this creates the illusion that you are on the surface of a sphere.
The value for the inter-planetary space is very large. Neverheless, wrap-arounds can even happen there if you fly far enough. Users have reported that strange things happen in that case as the game code is not really prepared for this. The central star and the planets still exist but the gameplay is broken.
In the world representing the inter-planetary space, the central star Solice is at position . All planets and moons (called celestial objects in the following) move with different angular velocities on circles of different radii (shown below) in the x/z plane around their parent object, i.e., Solice or a planet.
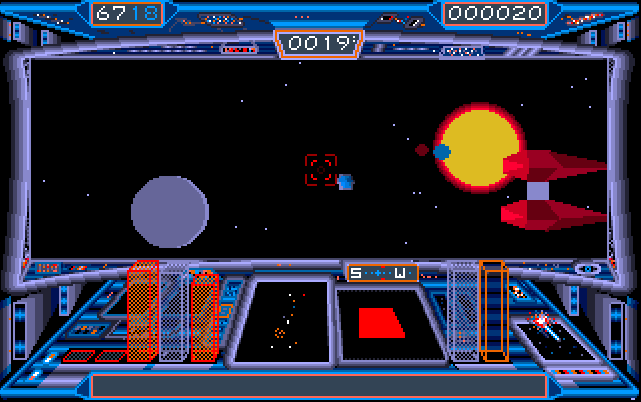 |
|---|
| The Icarus spaceship in space. The gray planet on the left is Apogee. |
When your spaceship is in space, the x/z positions of the celestial objects are periodically updated. However, when your spaceship arrives at a planet or moon, those updates are stopped and the current position of all celestial objects is saved to be restored later when you return to space.
| Celestial object | Orbit radius |
|---|---|
| Dante | |
| Vista | |
| Apogee | |
| Millway | |
| Aldos | |
| Enos | |
| Castron | |
| All seven Millway moons | |
| QBeta |
The periodic update of the celestial object positions happens in two steps. The game keeps track of the revolution of a celestial object around its parent object in an angle variable. In the game, all angles (including those used for 3D transformations etc.) are represented by integer values between 0 and 4095 to limit the size of the precomputed cosinus and sinus tables. A value of 0 corresponds to and a value of 4096 corresponds to , resulting in an angular resolution of . Each celestial object has a counter variable that is incremented in each update round. When the counter reaches a certain end value, the object’s revolution angle is incremented by its angular velocity. This reduces the number of position recalculations and allows to let the planets move slower than per update cycle.
// Calculates the x/z position of a celestial object.
// Note that each object has its own set of variables
// and constants.
counter++
counter &= endValue
if(counter==0) {
angle += angularVelocity
calculate relative position:
x = radius * sin(angle)
z = radius * cos(angle)
add position of parent object to x and z
}Furthermore, the calculations involve a lot of scaling operations (efficiently implemented as bit shifts) that we did not show in the algorithm above and that prevent that the 32-bit variables overflow due to the involved large numbers (remember that the orbit radii are all around or greater). To achieve the best accuracy for each celestial object, the game uses object-specific scale factors.
The distance of your spaceship to the sun plays an important role when you are flying in space. That distance on the x/z plane is approximated by where and are the x and z coordinates of your spaceship relative to Solice. This clever formula, which does not require any multiplication or division operation (the division by 3 is avoided by multiplying all the constants mentioned in the following explanations by 3), is obtained by approximating a circle by a slightly irregular octagon with corner points , and (for a radius of 1) as illustrated below for a quarter circle:
If and the y coordinate of your spaceship relative to Solice is in the range your spaceship’s shield energy will slowly drop, and your ship will overheat and finally explode.
Similarly, the game calculates your distance to Millway (using the same approximation as above), which is the largest planet in the system. If and the y coordinate of your spaceship relative to Millway is in the range , the high pressure of Millway’s atmosphere will slowly destroy your ship.
Unlike the surfaces of the planets and moons, the space world is empty when created, except for the sun, the celestial objects and some special game objects. All other game objects that you encounter in space, e.g. asteroids and pirate spaceships, are created randomly. When your ship is in motion, asteroids randomly appear in front of your ship with a probability that depends on your speed and whether the inter-planetary stardrive of the ship has been activated. Asteroids will appear with a much higher probability if and the y coordinate of your spaceship relative to Solice is in the range . This simulates an asteroid belt between Apogee and Millway.
The value of will also trigger the creation of random objects that appear near your spaceship with certain probabilities. They are shown below:
| Random encounters | |
|---|---|
| Columbus, Horatio, Tripuss, Small fighter, Egron Birdfighter, Large bird, Space ray | |
| between and | Whale, Proximity mine, Pirate ship, Columbus, Duck, Small fighter |
| between and | Old heap of junk, Scrap metal, Proximity mine |
| Starglider, Old heap of junk, Scrap metal, Bouncing bomb, Small fighter |
Apart from a few exceptions, everything you can see in the 3D view of the game is handled by its object system. This includes the buildings on the planet surfaces, the various ground and space vehicles, and even the tunnel walls when you are flying through a planet’s tunnel system. The only exceptions are the planet/moon surface itself (the ground and the check board pattern on it are painted separately from the objects) and the stars in the dark sky, which are painted as small dots.
Information on an object is stored in a 68-byte data structure. Around thirty bytes of that structure have the same meaning for all objects. Among others, those bytes contain
The object type defines the visual shape and behavior of an object. There are in total 148 object types, including the player’s spaceship and the different celestial objects. For example, type 30 is the Icarus spaceship, type 39 is a hovercar, and type 72 is a laserbolt fired by a weapon.
The other bytes in the structure contain type-specific information. For example, a Ground Based Laser Cannon — an enemy object that starts shooting at the player’s spaceship when it comes too close — keeps a countdown to the next laserbolt it will fire. To give you another exampe, homing missiles store a pointer to the object they are following in their object structure.
The game’s 3D engine has a table with enough space to hold 250 object structures. As already explained, the different worlds are isolated from each other, which means that each world has its own cordinate system and, apart from the the player’s spaceship, objects cannot move between worlds. When the player enters a world (i.e., space, or a planet’s or moon’s surface or tunnel system), the object table is reinitialized with a world-specific list of objects that contains
Typically, the initialisation list of a world only describes a few dozen predefined objects and their positions. The remaining empty slots (indicated by their object type field set to 0) in the 250-object table are used for dynamically created objects, such as randomly appearing enemies or fired laserbolts and missiles. Pointers to the empty slots are placed on a stack. In that way, creating a new object is a very simple operation and typically looks like this:
Object **top // pointer to the top of the free-object stack
...
if(numberOfFreeObjects>0) {
// pop pointer to free object slot from stack
Object *newObject = *(--top)
numberOfFreeObjects--
initialize the object structure fields
}You might have noticed in the above code that creating an object does not involve adding it to some kind of list of “active” objects. Such a list does indeed exist but it is not updated during the object creation process. To understand this, we have to learn more about the game’s main loop which roughly looks like this:
while(game is running) {
draw objects
handle gameplay (story events etc.)
handle user input
update objects
fire player weapons
check collisions
}The first phase, that is drawing the objects on the screen, involves passing through the object slots in the object table and compiling a list of all objects with object type different from 0, i.e., a list of all currently existing objects in the world. In fact, this operation compiles two lists, depending on how far the object is from the player:
foreach(slot "object" in object table) {
// check if slot is in use
if(object.type!=0) {
// calculate relative position to player.
// (the actual code is more complex because planet and
// moon surfaces are tori)
dx = abs(object.x - icarus.x)
dy = abs(object.y - icarus.y)
dz = abs(object.z - icarus.z)
// check distance
maxDist = look up in table depending on object.type
if(dx>maxDist || dy>maxDist || dz>maxDist)
add object to list of far objects
else
add object to list of close objects
}
} Only objects that made it to the list of close objects will be later drawn on the screen. The threshold is object type specific. While celestial objects are always drawn, small objects, like a small ground vehicle, are only drawn when they are relatively close.
The two lists also play an important role in the “update objects” phase of the game loop. In that phase, the game executes type-specific functions for each object. Depending on whether an object has been classified as far or close during the drawing phase, different update functions are used. For example, the update function for a close Egron Land Tank (object type 9) lets it turn toward the player’s spaceship and shoot at it. When being on the list of far objects, the tank’s update function basically only adds its speed vector to its current position, i.e., the tank just moves on a straight line on the planet surface. The update phase is also responsible for cleaning up destroyed objects and returning them to the pool (or, more precisely, the stack) of free object structures.
As a concluding simple example, the following code shows the “close” update function of a Proximity Mine (object type 2). Its “far” update function is empty.
updateCloseProximityMine(object) {
dist = abs(object.transformedZ)
if(dist<0x300) {
// explode!
object.explosionPhase = 0
// rock the Icarus around its z axis from the explosion
icarus.rotZChange += randomInt(-32..+32)
icarus.shieldEnergy = max(0, icarus.shieldEnergy-1500)
// update game statistics for the highscore table
numberOfIcarusHits++
}
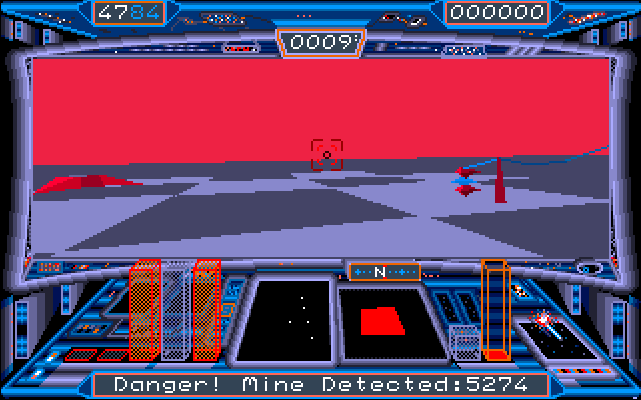
else if(dist<=0x600) {
showMsgWithObjectPosition("Danger! Mine Detected:", object)
}
object.rotY += 0x40
}Note that instead of calculating the distance between the mine and the player’s spaceship, the code uses the transformed z coordinate of the mine (the transformed z axis is the axis pointing into the scene from the player’s viewpoint) which is a sufficient approximation.
Objects are modeled as 3D polygon meshes. In total, there are 104 models representing the 104 types of objects that are (a) visible (there is an invisible object) and (b) not celestial objects (the latter are drawn as disks with a shadow zone on the side facing away from the central star). An object’s mesh consists of one or more polygon faces. A face can have up to 6 vertices (if it has only two vertices, it is drawn as a line) and a color defined by a color index in a game-wide fixed palette of 16 colors. There is also a special object (type 47) that constantly changes its colors.
Note: Although the original Amiga 500 and 2000 models were able to show graphics with up to 64 colors in 320x200 resolution, the game only uses 16 colors in order to reduce the number of bitmap drawing operations.
The polygon vertices are defined by indexes in a table of vertices. Interestingly, that table does not contain the x/y/z coordinates of the vertices. Instead, there is another level of indirection where the three components of a vertice are again 15-bit indexes in a table with 16-bit coordinate values. If the MSB (bit 15) of the coordinate index is set, the coordinate value is negated before being used as a vertex coordinate component.
face table:
vertex index 1 ----> vertex table
vertex index 2 coord index 1 ----> coordinate table
vertex index 3 coord index 2 coordinate values
... ...Object shapes can be animated. In that case, the object model contains more than one vertex table , each one corresponding to an animation frame with the same number of polygons but with different vertex coordinates. The model can define two animation ranges and with and . The rendering of the polygon mesh cyles first through frames using the vertex tables and then through .
For some objects, the animation is controlled by their update function. For example, the Egron Silo object, a large building with a door, is programmed to open its doors to let a spaceship leave the silo:
if(silo.hasCreatedShip) {
// ship destroyed?
if(silo.ship.type==0) {
// close the door
silo.animationPhase--
silo.hasCreatedShip = false
...
}
else if(silo.animationPhase==19) {
// door is completely open. let the ship fly away.
...
silo.ship.y -= 40
}
else {
// continue open-door animation
silo.animationPhase++
}
}
else {
...
// create a ship that will leave the silo
silo.ship = ...
silo.hasCreatedShip = true
}Objects also have a bounding box. Finally, objects can cast shadows on the planet/moon surface, which is an impressive feature given the age of the game. To this end, each object model contains a separate list of faces and vertices that are used to draw the shadow on the ground.
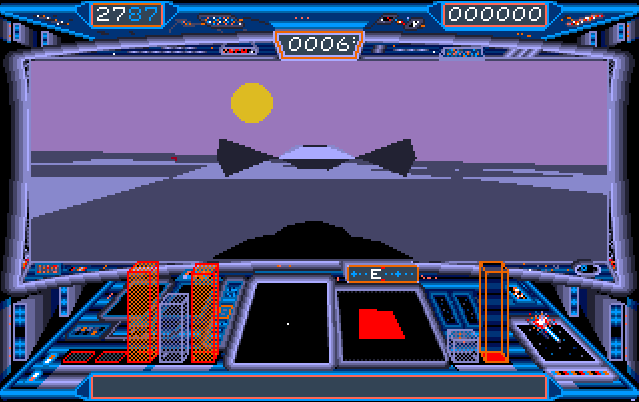 |
|---|
| The Icarus spaceship casting a shadow on the ground. Note that the shadow does not depend on a light source. It would be also visible with Solice in the sky. |
The complete 3D graphics routine of the game consists of the following steps:
To be continued